Quando submetemos um condutor metálico a um gradiente térmico em suas extremidades, a extremidade mais quente terá uma energia cinética maior e fará com que os elétrons dessa região se desloquem para o lado mais frio, gerando uma diferença de potencial (ddp) elétrico entre as extremidades do condutor na ordem de alguns milivolts (mV). Essa ddp depende da natureza dos condutores e da temperatura das extremidades.
Quando o gradiente de temperatura é linear, a diferença de potencial elétrico 
depende apenas do material e das temperaturas 
e 
, (
), formalmente representado pela fórmula:
depende apenas do material e das temperaturas e , (), formalmente representado pela fórmula:
onde
S é o coeficiente termodinâmico de Seebeck (mV/°C).
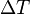é a diferença de temperatura 
e.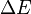
é a diferença de potencial elétrico usualmente medido em milivolts.
Agora se considerarmos dois matérias condutores diferentes A e B unidos pela junção J1 e j2 formando circuito fechado, quando submetidos a diferentes T1 e T2, os elétrons de um metal tendem a migrar para o outro ocorrendo uma circulação de corrente elétrica.
Se abrirmos o circuito em qualquer ponto e possível observar uma fem conhecida como tensão de seebeck. Mas para utilizarmos o par termoelétrico como medidor de temperatura podemos considerar o circuito abaixo
Os metais A e B estao unidos pela junção J1 chamada de junção quente ou junção de medição. A extremidade do metal A é unida ao instrumento de medição pela junção J3 e a extremidade do metal B é unida ao instrumento de medição pela junção J2. O ponto onde os fios se conectam ao instrumento de medição é chamado de junção fria ou de junção referência. Desde que as junções J2 e J3 estejam a mesma temperatura elas nao interferem na medição podendo ser consideradas uma unica junção.Assim considerando:
onde SA e SB são os coeficientes de Seebeck dos metais A e B, T1 e T2 representam a diferença de temperatura na junção dos materiais. Os coeficientes de Seebeck são não-lineares e dependem da temperatura absoluta, material, e da estrutura molecular. Se os coeficientes de Seebeck podem ser considerados efetivamente constantes numa certa gama de temperatura, a fórmula acima pode ser aproximada por:
Desse modo é possível obter-se energia elétrica usando-se uma fonte de calor.
